公司产品广泛 更重要的-九游娱乐(中国)有限公司-官方网站

一水 发自 凹非寺量子位 | 公众号 QbitAI

能拿下数学奥赛银牌水平的AI是否达到了12岁陶哲轩的水平？

陶神本东谈主的回答来了——

两三年后，AI将会在这些数学竞赛中比东谈主类作念得更好。（再过个两三年吧doge）

以上来自数学大佬陶哲轩在巴塞罗那的最新专访，既回复了一些大家现时最艳羡的AI议题，也不乏一些意旨探讨，比如：

把柄纳维-斯托克斯方程，水果真可能自愿爆炸并甩掉天下吗？AI可能甩掉东谈主类吗？如何看待AI掌合手在马斯克这么的富豪手中？……网友们看完后皆点头，纷纷暗示不愧是专科的：

听到一位贯通精明该主题的顶级数学家建议的更有把柄的不雅点令东谈主焕然如新。

更重要的，东谈主们对千禧年七浩劫题之一的纳维-斯托克斯问题也进行了最新表态。

成果令陶哲轩也感到不测：

（与2007年的成果比拟）看到东谈主们对纳维-斯托克斯问题的见解发生了变化，尤其令东谈主畏惧。

具体咋回事？底下咱们接着康康。

陶哲轩巴塞罗那最新采访

（以下为部分节选）

Q：你以为东谈主工智能组成的挟制可能甩掉东谈主类吗？

A：表面上是不错的。与以前的许多变革性技艺（如汽车、飞机、互联网）不同，东谈主工智能的特有性在于它渗入到了咱们活命的方方面面，如新闻、数学、医学等范畴。

但咫尺的技艺极其有限，它们基本上都是靠猜，或然能提供正确谜底，或但是透顶没用，是以我咫尺并不悼念。

不外在将来10年或20年内，东谈主工智能会变得愈加雄壮，但咱们也将同步加多更多隆重经历。

Q：把柄纳维-斯托克斯方程，表面上水不错自愿爆炸并甩掉天下吗？

A：在数学中，水可能会“爆炸”，但这远莫得听起来那么令东谈主隆盛。

这是数学模子中的“爆炸”自得，属于特定的数学特点（流体能量聚积），但并不料味着践诺天下会发生本色的爆炸。就像挥鞭时，鞭子顶端的速率会跨越音速，发出噼啪声，这在数学上称为“爆炸”，但本色上仅仅音爆效应。

这也施展在某些情况下，纳维-斯托克斯方程可能不再是流体的精粹模子。

Q：谷歌DeepMind几个月前秘书，其东谈主工智能系统AlphaProof和AlphaGeometry在外洋数学奥林匹克竞赛中取得银牌。

A：是的，但它们不是在认真比赛中。诚然成果足以拿到银牌，但并不透顶等同于东谈主类的比赛。

在确切的东谈主类比赛中，学生需要在8小时内处理沿路6个问题，而谷歌的AI竞赛需要疑望：率先它们有两个清闲的系统，且别离处理了3个和4个问题（非一次性处理沿路）；其次它们拿到的问题需要经由东谈主类翻译，且领有更多时刻。

Q：你12岁就取得银牌，东谈主工智能也曾达到12岁陶哲轩的水平了吗？

A：我以为在两三年内，东谈主工智能将会在这些数学竞赛中比东谈主类作念得更好。

诚然东谈主工智能在某些竞赛中短期内可能杰出东谈主类，但在像数学探究这么需要长久创造性的职责中，AI还远远无法取代东谈主类。要是咱们能处理如何让AI从极少数据中学习的问题，好像在两三年内，AI在数学竞赛中的发扬会杰出东谈主类。

Q：跨越你？短短三年？

A：是的，不外我也曾好多年莫得进入这类比赛了。这些竞赛一样于奥运会的百米短跑，而数学探究更像马拉松。处理一个探究问题可能需要几个月的时刻，还需要查阅多数文件。

Q：你以为东谈主工智能在数学探究这类具有创造性的步履中，能跨越你吗？

A：数学家取得告捷的原因之一是：有多数失败的经历训诫，这是AI不具备的。

AI擅所长理以前有多数数据的问题，能成为相配有效的助手。

但问题是，数学家们还有许多不为东谈主知的失败经历，而东谈主工智能莫得这些失败的数据，这导致其只擅所长理多数与之前问题一样的问题。

打个比喻，要是你要教AI识别一杯水，它需要数百万张水杯的图像手脚例子。这亦然我刚才提到的——要是能让AI从极极少数据中学习，它好像在创造性任务上也能杰出东谈主类。

Q：您如何看待东谈主工智能掌合手在像埃隆·马斯克这么的超等富豪手中？

A：像东谈主工智能这么进击的技艺不应该由一两家公司摆布。

诚然构建大型AI模子需要多数的资金和资源，但基本技艺是公开的，将来会有更多通达的AI替代决议出现。

同期，咱们必须对AI进行适宜监管，尤其是在搪塞AI生成的深度伪造内容时。

要是一切都不错伪造，咱们如何让某东谈主敬佩某事发生了？咱们需要找到新的边幅来考证信息的真实性。

愈加敬佩“流体中存在有限时刻奇点”

就在最近，陶哲轩赴巴塞罗那进入了“交互中的流体能源学、几何和打算机科学”会议。

会中发起了一项对于“流体中是否存在有限时刻奇点”的投票：

在欧几里得3维空间中，欧拉和纳维-斯托克斯方程（具有平滑驱动条款）是否会出现存限时刻奇点？

参与者需要按照从0-10进行投票，其中0代表坚决狡赖，5代表不细目，10代表坚决认可。

投票率先以暗里边幅进行，其中蓝色代表欧拉方程，红色代表纳维-斯托克斯方程。

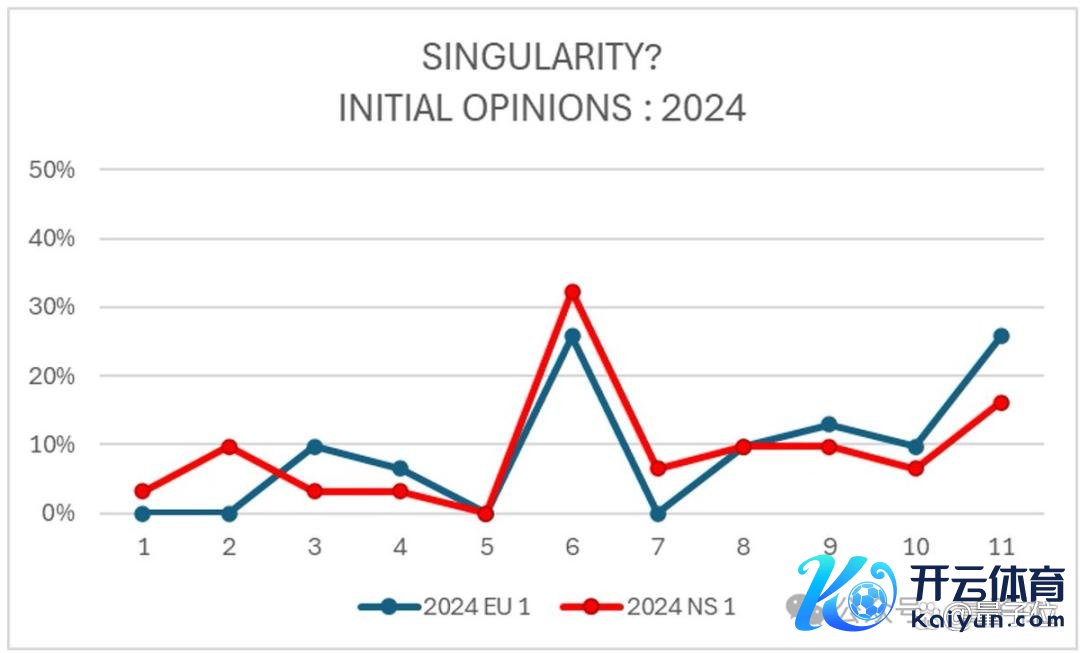
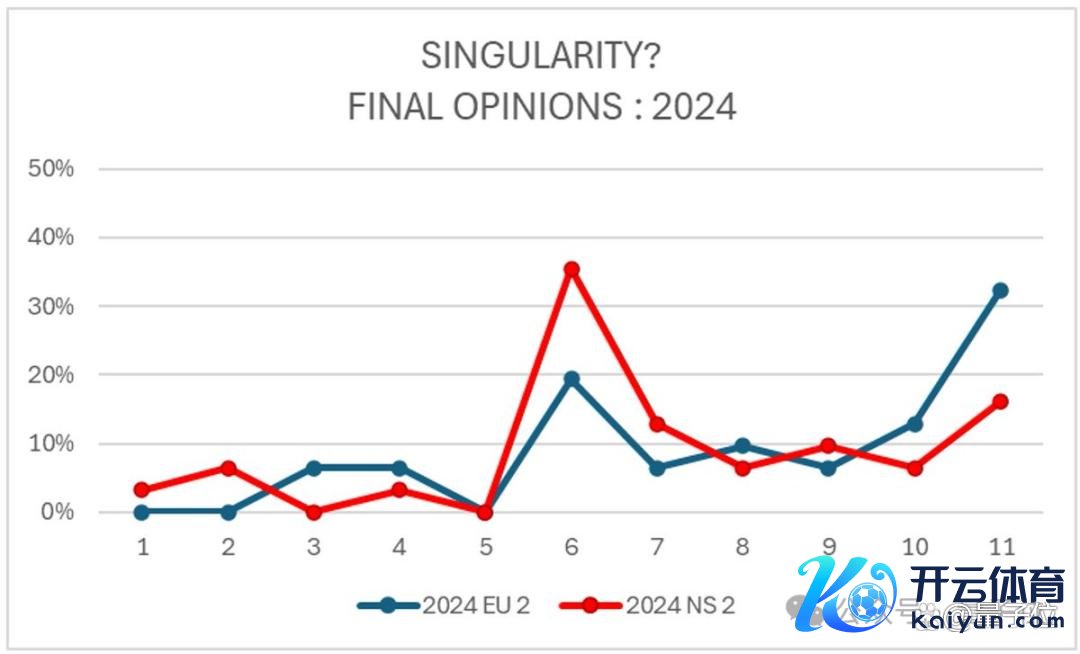
随后又进行了公开举腕表决，意图通过两种边幅来反应一种动态的意见造成经过。

值得疑望的是，其时好多东谈主都把眼神投向了陶哲轩。

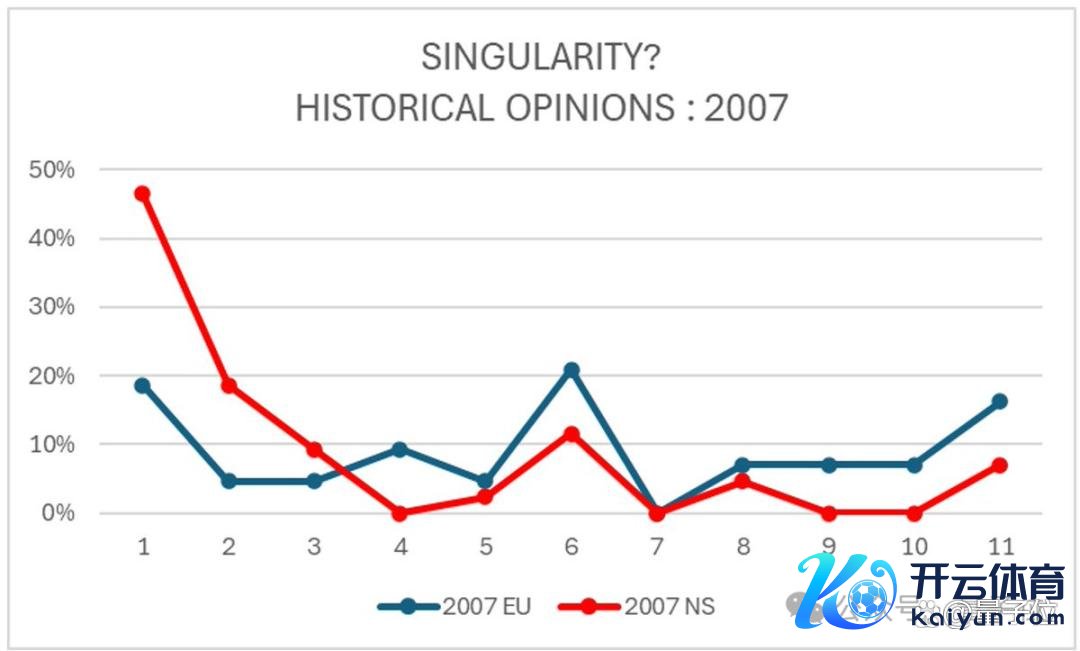
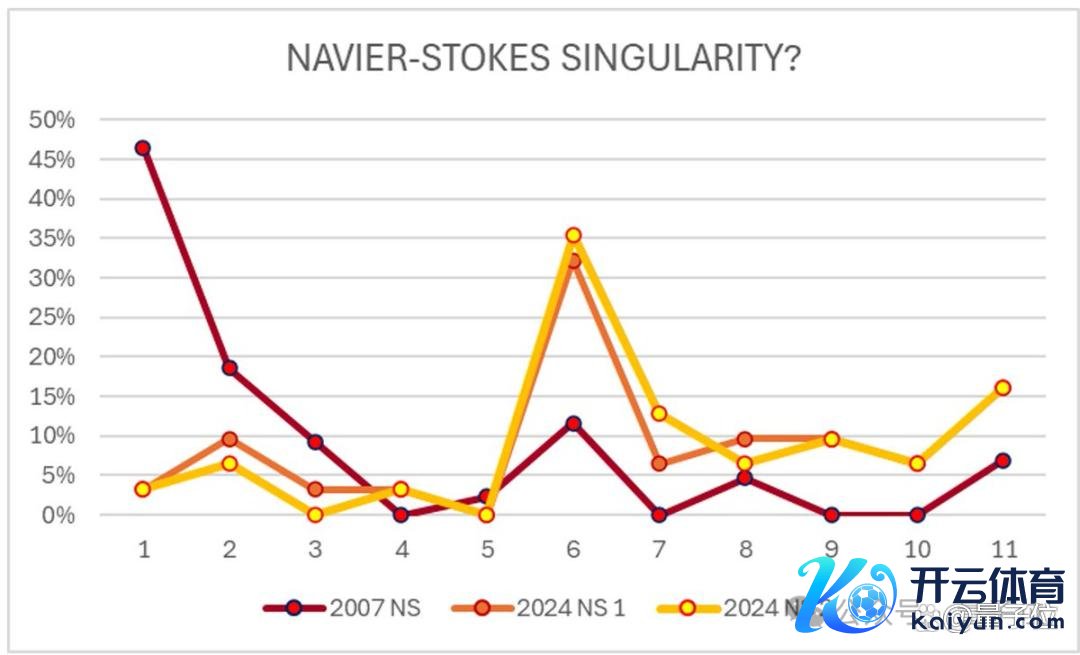
对比2007年，其时在瑞士奥苏瓦举行的欧拉方程250周年挂念会议上，有对归拢问题的投票拜访。

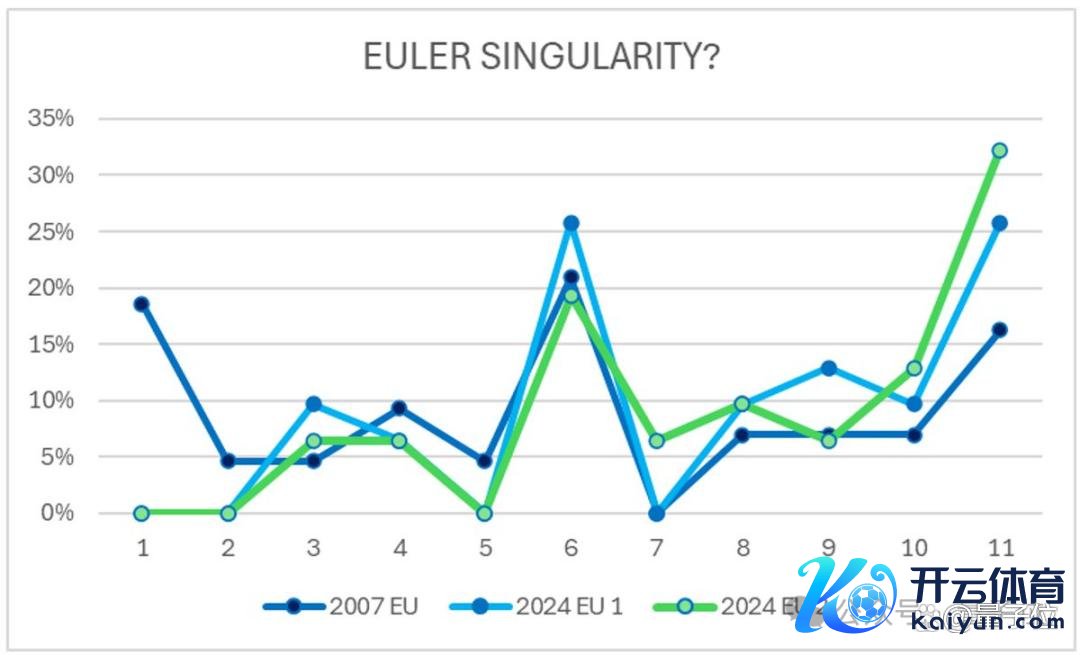
重叠上述成果，不错看到大家们对于归拢问题在不同时代、两种不同所在下的投票作风各异。

不错得出以下不雅察论断：

意见也曾更多地倾向于奇点意见因受到周围东谈主的影响而及时篡改，这与信息流动相配联系

对此，你如何看？

参考联贯：[1]https://english.elpais.com/science-tech/2024-10-12/terence-tao-mathematician-its-not-good-for-something-as-important-as-ai-to-be-a-monopoly-held-by-one-or-two-companies.html[2]https://x.com/robertghrist/status/1836755464618434938[3]https://mathstodon.xyz/@tao/113165731590588489公司产品广泛